并查集笔记
最近在读另一本经典的算法教材：Algorithms(4th edition, Robert Sedgewick and Kevin Wayne），相比其他算法教材，这本书有几个特点：
1.图示非常丰富，阅读起来更有趣，更易懂；
2.给出了测试算法用的不同规模的数据和测试方法，以及展示算法结果所需要的工具。这些工具使得算法的测试、结果展示非常方便、直观。
3.介绍问题时更自然，相比算法导论定义、证明的方式，本书给出算法的应用场景，对需要解决的问题，不断改进算法得到最优结果，逐步改进的思路符合人们研究问题的正常过程，思维不跳跃，使学习过程有逻辑可循。
这本书有一个配套网站，http://algs4.cs.princeton.edu/home/，网站上除了提供书的部分内容，程序和数据下载外，还提供了课程的幻灯片和一些算法过程展示视频，效果非常赞。
下面是我对书中1.5节Case Study:Union-Find一节所做的笔记，可以部分反映出这本书的特点。
</br>
问题引入：动态连通性(Dynamic connectivity)
输入是一系列整数对，其中每个整数代表某种类型的对象，我们将整数对p q的含义解释为“p和q连通”。连通是一种等价关系，即满足：
自反性：p和p连通；
对称性：如果p和q连通，那么q和p连通；
传递性：如果p和q连通，q和r连通，那么p和r连通。
等价关系将所有对象分成等价类：如果两个对象连通，则它们属于同一个等价类。
我们的目标是：用程序过滤掉输入序列中不连通的数对。换句话说，当程序读入一对数p q时，只有当根据已经读取的所有数对不能说明p q连通时，才将p q数对输出，否则如果能判断出p q连通，则忽略p q数对，继续读下一对数。
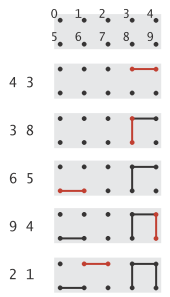
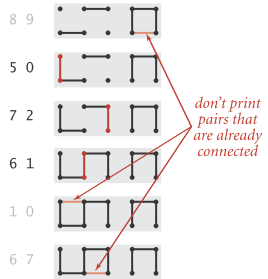
用下图说明问题，图中有10个点，左侧数字为每次读入的连通数对。红色边为根据最新读入的数对产生的新边（即此时应输出这个数对），注意第二幅图当输入8 9时，由于8 9已经连接，因此不在8 9节点中增加新边（即不输出8 9数对）。连通完成后，图中左侧的三列点和右侧两列点分别为等价类。
上面描述的动态连通性问题在几个领域有许多应用，如在网络中：
1.输入的整数代表网络中的计算机，数对代表网络中的连接。我们的程序用来判断为了让p和q通信，是建立一个新的直接连接，还是可以用已有的连接建立通信路径；
2.整数代表电子电路中的连接点，数对代表连接各点的线路；
3.整数代表社交网络中的人，数对代表好友关系。
在这些应用中我们可能需要处理数百万的对象和数十亿的连通关系。
术语
为了便于讨论，用网络术语定义问题。我们称上面的对象为点，称数对为连接，称等价类为连通组件，简称组件。简单起见，假设我们有N个点，每个点用整数命名，从0到N-1。
下图是一个规模大一些的连通性问题实例，从中可以看出连通性问题的困难之处。
图中有625个点，很容易看出左下角的5个点是一个组件，但是并不容易判断任意两点的连通情况。对程序来说任务难度可能更大，因为程序只能处理点的名字和连接，并不能获得图标的几何结构。怎样才能快速判断给定的两个点是否连通呢？
问题精确定义（API）
为了解决问题，第一步工作是给出问题精确的定义。通常我们对一个算法的需求越多，用来实现它的时间和空间就越多，困难也越大。因此需要给出适当的定义。
为了定义问题，用一套API来封装所需要的基本操作：初始化；为两个点增加链接；标识包含一个点的组件；判断两个点是否属于同一组件；给组件计数。我们得到以下API：
[code lang=”java”] //Union-find API public class UF UF(int N) //initialize N sites with integer names (0 to N-1) void union(int p, int q) //add connection between p and q int find(int p) //component identifier for p (0 to N-1) boolean connected(int p, int q) //return true if p and q are in the same component int count()// number of components [/code]
定义API使得实现一个解决动态连通性问题的算法简化成了实现上述API。
用数组id[]记录每个点所属的组件，一般用一个组件中的某个点作为组件的标识符。初始时，每个点为一个组件，所以对i从0到N-1将id[i]置为i。
并查集API的基本实现如下，算法维护两个实例变量：组件的数目和数组id[]。不同的算法区别在于find()和union()的实现。
[code lang=”java”] public class UF{ private int[] id; //组件标识数组 private int count; //组件数量
public UF(int N){
id = new int[N];
for(int i = 0; i < N; i++)
id[i] = i;
count = N;
}
public void union(int p, int q){}
public int find(int p){}
public boolean connected(int p, int q){
return find(p) == find(q);
}
public int count(){
return count;
}
public static void main(String[] args){
int N = StdIn.readInt();
UF uf = new UF(N);
while(!StdIn.isEmpty()){
int p = StdIn.readInt();
int q = StdIn.readInt();
if(uf.connected(p, q)) continue;
uf.union(p, q);
Stdout.println(p + " " + q);
}
} } [/code]
测试方法
UF类中提供了供测试用的main方法，它读取输入的整数对，如果数对没有连通，就将其连通并输出此数对。
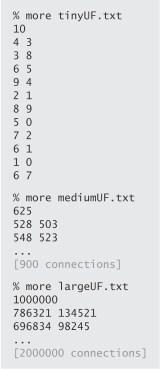
提供了3个不同大小的测试数据集：tinyUF.txt包含10个点的11个连接，mediumUF.txt包含625个点的900个连接，largeUF.txt包含100万个点的200万个连接。数据的形式为：
每个数据第一行为总点数，剩下各行是各个连通的数对。
算法分析方法
为了分析算法，关注每个算法访问（读或写）数组元素的次数。
算法实现
下面给出三种算法实现，并逐渐提高性能。
（一）Quick-find
第一种方法维持的不变式是：当且仅当id[p]和id[q]相同时，p和q才是连通的。即同一个组件中的点有相同id[]值。这一方法称为quick-find，因为find(p)只返回id[p]，一次访问id[]即可完成。为了维持此不变式，操作union(p, q)时，首先检查p,q是否属于同一组件，如果不属于，则修改p、q组件中点的id[]，使所有id[]项相同。例如：
上图中，p=5,q=9，p和q原本属于不同组件，将它们连通时，将p所在组件的标识改为8，使得连个组件标识一致，成为同一组件。
算法实现
[code lang=”java”] pubic int find(int p){ return id[p]; }
public void union(int q){ int pID = find(p); int qId = find(q); if(pID == qID) return; for(int i = 0; i < id.length; i++){ if(id[i] == pID) id[i] = qID; } count–; } [/code]
性能分析：
find()操作很快，因为每次操作只访问id[]一次。但是union()操作每次都需要遍历id[]一遍，因此quick-find算法对大数据量问题不适用。
quick-find算法每次find()操作需一次数组访问，每次union()需要N+3到2N+1次数组访问（每次union()，需要两次find()，测试id[]中所有项，并更改其中1到N-1个项）。
考虑一个动态连通性问题最终得到一个单个组件，需要至少N-1次union()，即至少$$(N+3)(N-1)\sim N^2$$次数组访问，即quick-find是平方阶时间复杂度的算法。对大数据量，如largeUF.txt，quick-find无法解决问题，因此需要更好的算法。
（二）Quick-union
下一个算法考虑加速union()操作，它使用和前一个算法相同的数据结构id[]，但是对id[]的值有不同用法：每个点的id[]项是该点所在的组件中另一个点的名称（可以是该点自己的名字），称这样的连通为链接（link）。
为了实现find()，从给定点开始，沿着它的链接到另一个点，再沿着这个点的链接到又一个点，这样一直继续直到到达根节点，即一个链接到自己的点。
这个算法的不变式是：当且仅当两个点的find()过程到达同一个根，这两个点属于同一个组件。
为了维持此不变式，union(p, q)操作沿着链接分别找到p和q的根，然后通过将其中一个根链接到另一个根，使得其中一个组件重命名，两个组件合成一个，这一算法称为quick-union。在合并根节点时，任意选择是重命名包含p的组件或是包含q的组件。
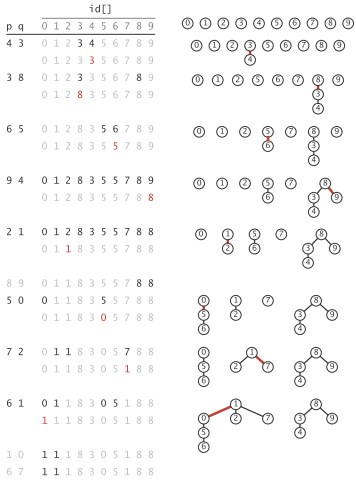
下图显示了以tinyUF.txt作为测试数据时，quick-union的执行过程：
quick-union算法的id[]实际上实现了树的森林表示，id[]项是指向父节点的链接，根节点有指向自身的链接。森林中的每棵树是一个组件，根为该组件的标识。
算法实现
[code lang=”java”] pubic int find(int p){ while(id[p] != p) p = id[p]; return p; } public void union(int q){ int pRoot = find(p); int qRoot = find(q); if(pRoot == qRoot) return; id[pRoot] = qRoot; count–; } [/code]
性能分析
quick-union似乎比quick-find快速，因为对每个输入数对，它不需要遍历整个数组，但是具体快了多少？在最优情况下，find()只需要一次数组访问获得组件标识；最坏情况下，find()需要2N+1次数组访问。具体性能依赖于输入的情况。我们在此不进行quick-find和quick-union的比较分析，因为接下来会研究一个更好的算法。在此可以认为，quick-uinon比quick-find有所提高，因为quick-find的union操作总需要线性时间，而quick-union并不总需要（取决于输入）。
find()操作的数组访问为1加上当前点的2倍深度；union()和connected()的数组访问次数是两个find()操作（如两个点属于不同树，union操作需要再加1）。
考虑quick-union的最坏情况，一个最终合为一个组件的动态连通性问题，输入数对的依次是0-1，0-2,0-3等等，N-1个这样的数对后，我们得到N个点组成的一个组件。由quick-uion生成的树高度是N-1，从叶子到根，依次是0,1,...N-1，对0 i数对的union()操作，数组访问次数是2i+2，因此对N-1个数对，数组访问总次数为$$N^2$$阶。
（三）Weighted quick-union
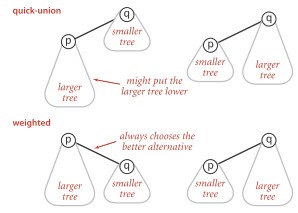
通过简单修改quick-union算法，可以保证quick-union算法的最坏情况不会发生。和quick-union任意的选择第二课树连到第一棵树不同，通过记录每棵树的大小，每次将较小的树连到较大的树上。这个算法称为加权(weighted)quick-union。
下图说明quick-union和weighted quick-union的区别：
上图可以看出：quick-union的连通策略使得生成的树趋于不平衡，进而使find操作所需时间越来越长；而weighted quick-union 总将小树连向大树，树的平衡性更优，避免性能恶化。
算法实现
[code lang=”java”] public class WeightedQuickUnionUF { private int[] id; private int[] sz; private int count;
public WeightedQuickUnionUF(int N){
count = N;
id = new int[N];
sz = new int[N];
for(int i = 0; i < N; i++){
id[i] = i;
sz[i] = 1;
}
}
public int count(){
return count;
}
public boolean connected(int p, int q){
return find(p) == find(q);
}
private int find(int p){
while(p != id[p]) p = id[p];
return p;
}
public void union(int p , int q){
int i = find(p);
int j = find(q);
if(i == j) return;
if(sz[i] < sz[j]){
id[i] = j;
sz[j] += sz[i];
}
else{
id[j] = i;
sz[i] += sz[j];
}
count--;
} } [/code]
性能分析
命题：由weighted quick-union生成的N个点组成的森林中，任意一点的深度最大为logN。(证明：略，见原书p229）。
推论：对N个点采用weighted quick-union算法，find(),connected()和union()的最坏情况时间复杂度是logN.
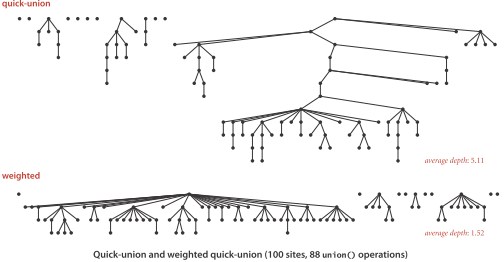
下图展示了对100个点规模的动态连通性问题，经过88次union()操作后，quick-union和weighted quick-union的对比：
从中可以看出，加权后的算法，森林中树的高度明显更低，只有很少的点离树的根较远。
三种算法性能对比
| 算法 | union | find |
| quick-find | N | 1 |
| quick-union | tree height | tree height |
| weighted quick-union | lgN | lgN |
| impossible | 1 | 1 |
总结
Algorithms一书更容易让人体会到学习、使用算法的快乐之处。如果你在《算法导论》的数学证明中有些疲倦时，不妨找来这本书，重拾初学者的乐趣。
