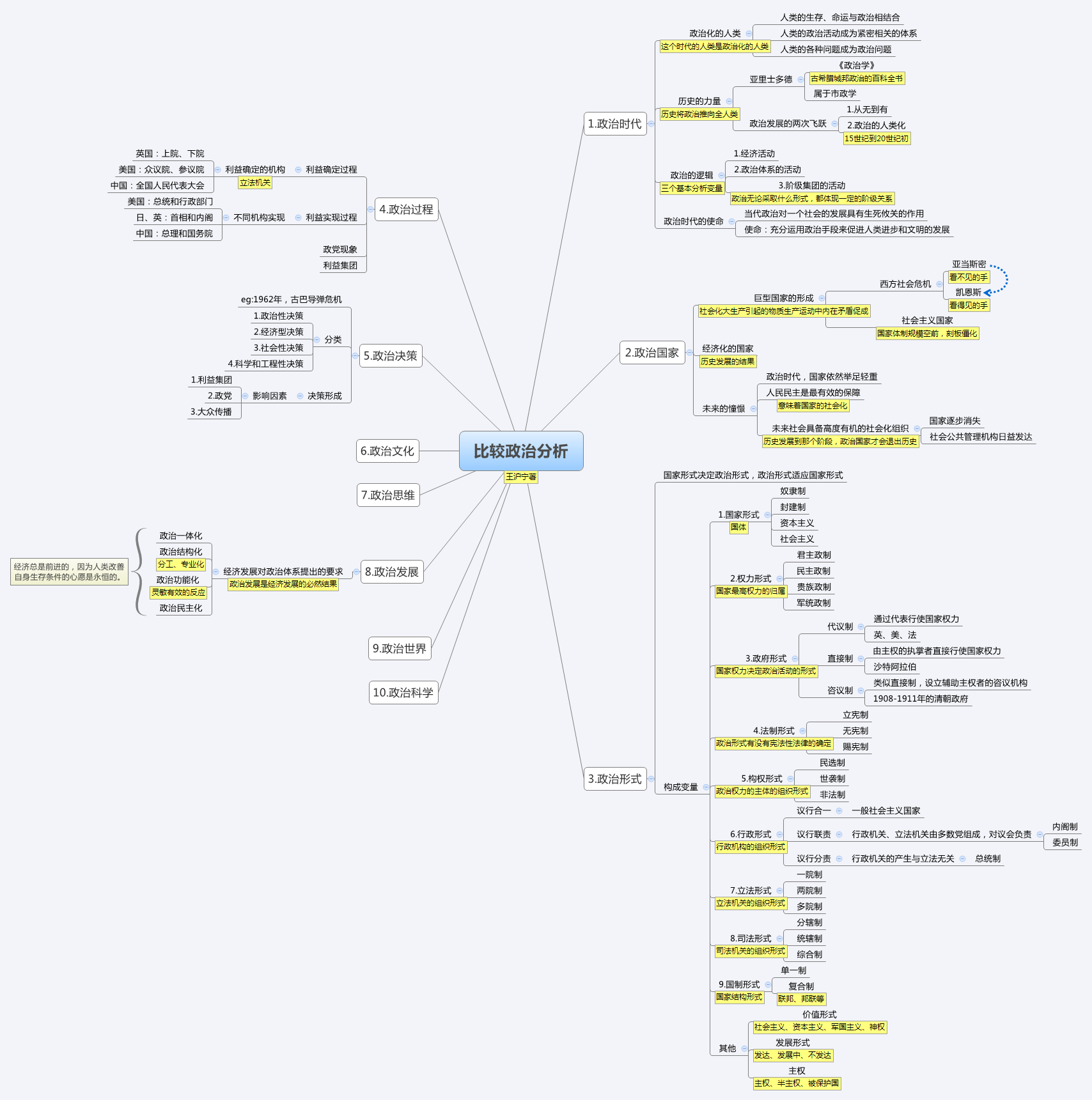
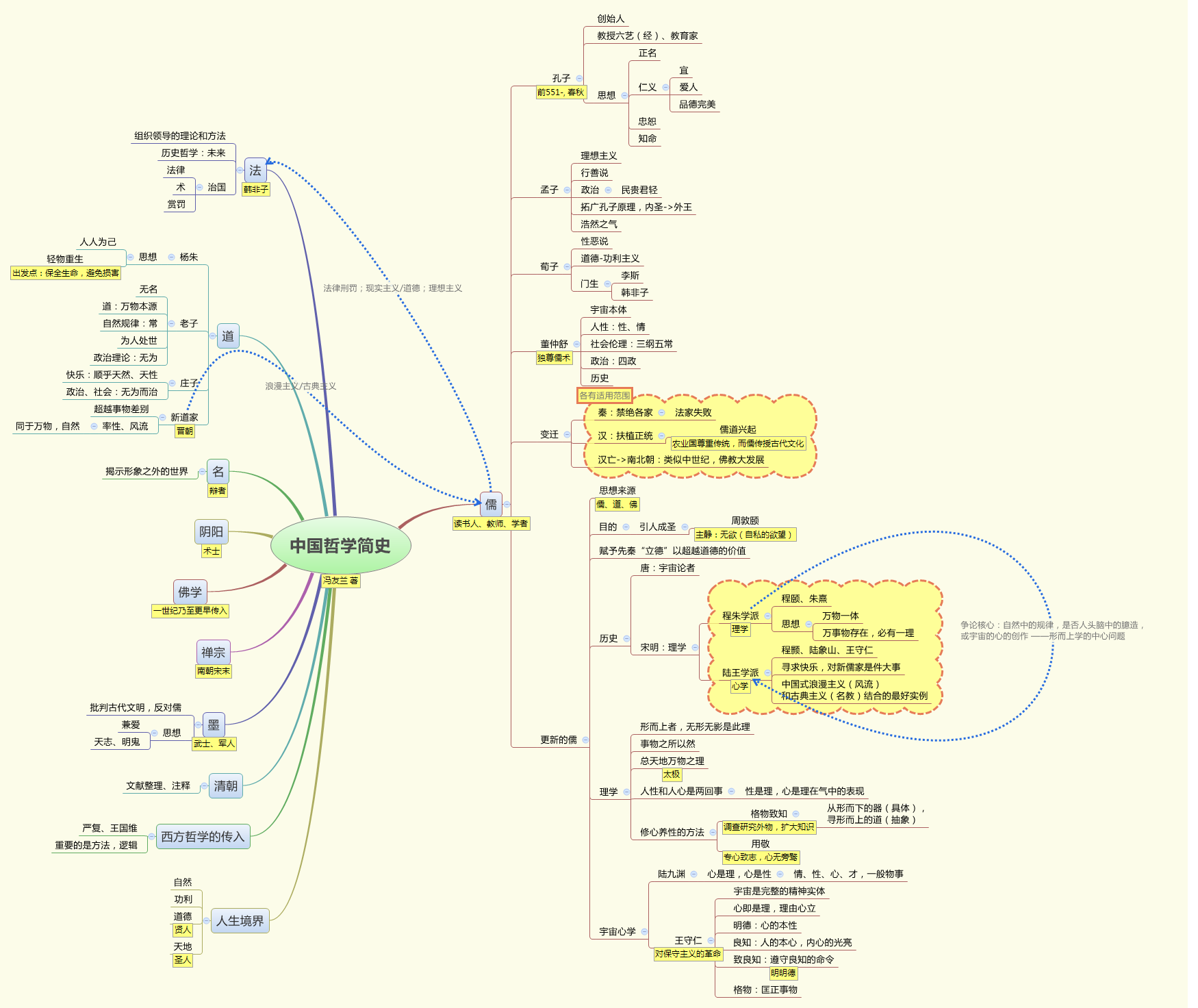
并查集笔记
</br>
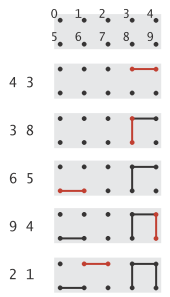
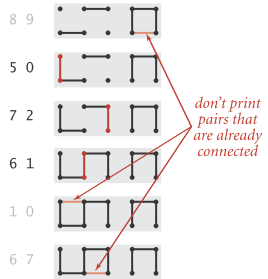

[code lang=”java”] //Union-find API public class UF UF(int N) //initialize N sites with integer names (0 to N-1) void union(int p, int q) //add connection between p and q int find(int p) //component identifier for p (0 to N-1) boolean connected(int p, int q) //return true if p and q are in the same component int count()// number of components [/code]
[code lang=”java”] public class UF{ private int[] id; //组件标识数组 private int count; //组件数量
public UF(int N){
id = new int[N];
for(int i = 0; i < N; i++)
id[i] = i;
count = N;
}
public void union(int p, int q){}
public int find(int p){}
public boolean connected(int p, int q){
return find(p) == find(q);
}
public int count(){
return count;
}
public static void main(String[] args){
int N = StdIn.readInt();
UF uf = new UF(N);
while(!StdIn.isEmpty()){
int p = StdIn.readInt();
int q = StdIn.readInt();
if(uf.connected(p, q)) continue;
uf.union(p, q);
Stdout.println(p + " " + q);
}
} } [/code]
测试方法
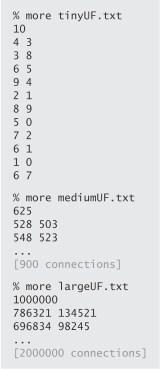

[code lang=”java”] pubic int find(int p){ return id[p]; }
public void union(int q){ int pID = find(p); int qId = find(q); if(pID == qID) return; for(int i = 0; i < id.length; i++){ if(id[i] == pID) id[i] = qID; } count–; } [/code]
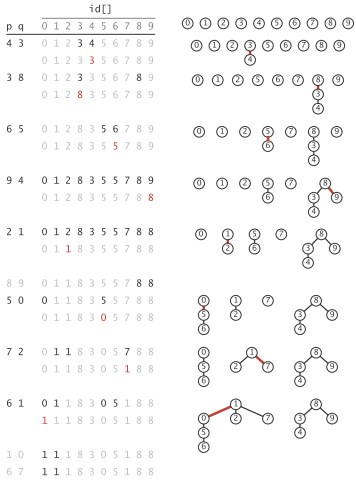
[code lang=”java”] pubic int find(int p){ while(id[p] != p) p = id[p]; return p; } public void union(int q){ int pRoot = find(p); int qRoot = find(q); if(pRoot == qRoot) return; id[pRoot] = qRoot; count–; } [/code]
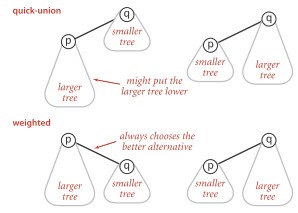
[code lang=”java”] public class WeightedQuickUnionUF { private int[] id; private int[] sz; private int count;
public WeightedQuickUnionUF(int N){
count = N;
id = new int[N];
sz = new int[N];
for(int i = 0; i < N; i++){
id[i] = i;
sz[i] = 1;
}
}
public int count(){
return count;
}
public boolean connected(int p, int q){
return find(p) == find(q);
}
private int find(int p){
while(p != id[p]) p = id[p];
return p;
}
public void union(int p , int q){
int i = find(p);
int j = find(q);
if(i == j) return;
if(sz[i] < sz[j]){
id[i] = j;
sz[j] += sz[i];
}
else{
id[j] = i;
sz[i] += sz[j];
}
count--;
} } [/code]
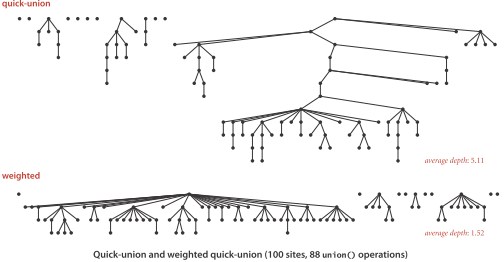
| 算法 | union | find |
| quick-find | N | 1 |
| quick-union | tree height | tree height |
| weighted quick-union | lgN | lgN |
| impossible | 1 | 1 |
windows下使用makefile示例
一、环境准备
1.安装MinGW 2.修改环境变量,把%MinGW%/bin添加到path中(%MinGW%为MinGW安装路径) 3.把%MinGW%/bin中的mingw32-make.exe复制,并重命名为make 验证上面三步是否成功: 在cmd窗口中输入,make -v,如果输出make版本信息则安装正确。
二、makefile测试 1.在准备测试的路径(如 C:\Users\James\test)下新建如下两个代码文件: [code lang=”c”]//—————————main.c : —————————// #include "stdio.h" main() { func(); printf("this is main\n"); getch(); }[/code]
[code lang=”c”]//—————————func.c : —————————// #include "stdio.h" func() { printf("this is func\n"); getch(); }[/code]
2.新建makefile文件: [code lang=”c”] test:main.o func.o gcc -o test main.o func.o func.o:func.c gcc -c func.c main.o:main.c gcc -c main.c [/code]
注意:上面的gcc -o和gcc -c前面必须是TAB,不是空格,否则运行make时会报错:“makefile:2: *** missing separator. Stop.”。
3.在cmd中切换至当前路径(C:\Users\James\test)下,运行make命令,输入: make 回车。 make命令执行的结果为: [code lang=”c”]C:\Users\James\test>make gcc -c main.c gcc -c func.c gcc -o test main.o func.o[/code]
此时路径下已经编译生成了test.exe,输入test即可看到运行结果。
本文主要参考了[1],windows下的各版本gcc介绍可以参考[2],makefile入门可以参考陈皓的《跟我一起写 Makefile》[3].
参考资料 [1]windows下使用makefile编译C语言: http://blog.csdn.net/zhanghan3/article/details/1334308 [2]gcc for Windows开发环境介绍, http://blog.csdn.net/Mobidogs/article/details/1819084 [3]跟我一起写 Makefile,http://blog.csdn.net/haoel/article/details/2886
离乡情怯
春节假期结束了,火车行驶了四十几个小时,把我从寒冷的西北又带到了温暖的南方,从家带向了学校。
下了火车,用了半个小时才买到广州地铁的车票,我背着装满厚衣服的书包,拎着箱子挤进了车厢。背上的书包不时碰到别人,我一边道歉一边取下包,站稳了位置。这时后边有人推我,我知道他要往前走,让出一个位置。一对年纪六十上下的大叔大妈提着大包小包挤了过去,车座上的人连忙让座,他们坐了下来放置好行李。
大叔出了一头的汗,站着的乘客好心,递给他几张纸巾,他接过来擦拭额头上的汗水,同时感叹广州已经有些热的天气,给他纸巾的大姐用广式普通话应答着。我欣慰于广州市民的热情,联想起北京有些公交上售票员对扛着行李的外地人的态度。
终于喘了口气,老两口感叹着进地铁的不易,大约是过验票口时遇到了点困难。
我打量着他们,头发白了一多半,身体还健康,看穿着应该是从小地方来的。他们带着三个捆扎起来的纸箱和两个包,我根据箱包的大小排列组合了几次才得到两个老人提这几件行李的方式。
想必箱子里都是家乡的土特产,而他们应该是来看儿女的吧。
他们的儿女为什么不来接站呢?哪怕上班也要请假来啊,从过惯了的家乡到大城市并不是件容易的事,对两个老人。
我想着他们的儿女,突然想起了我的父母。想起出门前,我对父亲说,爸,我走了;想起在汽车站,我对母亲说,妈,再见。
泪水在眼眶里打转,我赶紧假装是空调的风吹到了脸,一边扭头一边庆幸没人注意到我的窘境。
离开家时似乎坚强,到了这里却开始思乡。
地铁到终点站了,老人家拿好行李,我也重新背起包,各自汇入了城市滚滚的人流中。
Book note:《我是沃兹》
父亲告诉我的方式是:不要死记硬背零件如何形成电路,而是理解电子流动在哪里才形成有用的电路;不要仅仅阅读线路图或是书上的内容,而要真正心领神会。
因为我已是成年人,有我自己的道德观——深刻关注人民的生活疾苦。我开始寻找生活真谛——如今我仍在这样做——我行事做人只为自己和他人拥有一个快乐的人生。
对政府行为,我所感受的震惊和恶心非笔墨所能形容:他们将我们的人生玩弄于股掌之间,并非如父亲所说,他们关心民众疾苦。
我具有幽默感,对生活我也保持这样的态度,只有快乐会成为我的选择。我认为是否快乐,取决于自己,只是自己。
我相当清楚自己要成为一位设计电脑的工程师,一位编写软件的工程师,一位风趣的工程师,一位愿意教授他人的工程师。
我清楚自己从不想玩社交游戏。即使到22岁,我也如此肯定自己并不想从工程领域调至管理层。我不愿进入管理层,进行政治性的争斗,或是踩着别人的肩膀往上爬。
大多上白班的人都喜欢在回家做些完全不同的事情。有些喜欢在家看电视,但我则喜欢做电子工程。我热衷于此,并以此为乐。
在我心中,道德举足轻重,至今我仍不能真正明白他为何对我撒谎。但是,大家都知道任何人是不同的。
在我心中,欢笑的人生远比掌握管理权重要得多,不过这只是我的观点。我认为快乐是人生中最重要的事,这样的人似乎有点傻傻的,但却是快乐的,这就是我一直以来想要成为的人。
这也是我为何从不会将《突出重围》事件放在心上的原因。即使你不赞同,甚至认为我们的关系出现裂痕,也不必认为我们相互为敌,只是性格不同罢了,而这就是快乐生活的最好方法。
我认为,人们对功能由许多需求,我们不应该限制人们的期望。
因为创建苹果公司,所以我能得到比维持生存更多的钱。我一生中从未打算赚一笔很大的钱。我常被那些为了在生活中创造更多事物的人们的故事所激励。
我记得我父亲那时告诉我,是教育能让我们提升到在生命中想要的高度,也能提升人的价值。
无论到哪儿,我都十分关注孩子——婴儿、幼儿、小孩子、大孩子。我试着跟他们交流,向他们微笑,给他们讲笑话,成为他们的玩伴。我自幼就被灌输这样一个想法:有”坏人”会伤害或绑架孩子,所以我决定成为一个”好人”,任何一个遇到的孩子都可以依靠的”好人”。
我喜欢小孩子们看着我的脸——简直是热爱。 我愿意给像我当时那样的年轻人有价值的建议,那些认为自己”格格不入”的、内心热爱设计和发明以及制造的年轻人,从而改变人们做事的方法。
当你发现你渴望实现你脑子里的主意时,我的建议就是关于这时你该做些什么的。你年轻、没钱,拥有的就是你脑子里的东西。你认为你脑子里的想法是好东西。这些想法就是你成天思考的东西,它们驱动着你。
但是,想发明些东西,与真正发明些东西,仍大有不同。比如,你怎么做这个,你怎样改变这个世界?
第一,你需要相信你自己,不要动摇。
有一些人——我提到的大多数人,尤其是你将要遇到的那些人的思维,通常都是非黑即白型。许多人看事情是从媒体或他们朋友看问题的角度来看的,如果他 们觉得媒体或朋友的观点是正确的话,那么其他人的观点就是错误的。所以,一个新想法——革命性的新产品或产品功能不会被许多人理解,因为他们看问题是用极 其简单的二分法。他们无法理解某样东西,可能是因为他们无法想象它,或者别人已经告诉他们什么是有用的或好的,而在他们听见的这些东西里面,并不曾包括你 的想法。
不要让这些人打消你的积极性。记住,他们只是用符合当时大众文化标准的观点来看问题。他们只看到了那些摆在他们面前的东西。这是种偏见,确切的说,这是一种绝对阻碍发明精神的偏见。
但这个世界不是黑白二分这么简单,中间还有许多灰色过渡。作为一个发明者,你必须看到事情的灰色过渡层次。你应当思想开明,不要人云亦云,根本不要 管大众的想法。你要保持客观,忘记自己听到的各种观点,清扫桌面,像一个科学家那样做实际的研究。你不要想一蹴而就,很快得出结论,然后尽可能地找论据来 证明自己的观点。谁会浪费时间支持一个糟糕的想法呢?顽固地坚持己见是不值得的,不要为此找任何理由。
得到能改变世界的新主意的唯一途径是,跳出现有的其他人的思维局限。你必须跳出其他人已经设置的人为障碍。如果你想想出别人以前从没想过的主意,你就得认识到一个有灰色层次过渡的世界,而不是只生活在黑白两色世界里。
为什么我说工程师像艺术家?工程师经常努力把事情做得更完美,甚至超乎他们的设想。……我们不停的加添代码,像一个画家用笔刷加添色彩,一个作曲家 加添音符。这就是到达完美的途径——努力使每件事完美地组合在一起,以一种前人未曾做过的方式。这使得工程师或其他人成为真正的艺术家。
在我一生中,我看到在每20位工程师中,才有一位能体现这种艺术家完美主义的人。所以让你的工程师工作成为艺术,是一件鲜见的过程,但这是我们应该努力达到的境界。我最近被电影《一往无前》(Walk the Line)所感动。在电影里,制作人告诉约翰尼·卡什,要带着”这首歌能拯救全世界”这样的想法来演奏它。
这总结了我在讨论设计和其他事物中的艺术时追求的许多东西。
如果你是那种罕见的工程师,兼具发明者和艺术家的素质,我将给你一些也许实现起来很难的建议:单独工作。
当你当家做主,决定自己要创造什么、如何去创造、如何协调功能和质量时,它就是你自己的一部分,就像一个你深爱着的孩子,想抚养他成长。你有巨大的动力创造最好的可能的发明——你以一种热情关心着它们,一种其他人命令你创造什么发明时不可能有的热情。
我现在十分自豪。我十分自豪。不仅仅是因为苹果翻身了,还因为它是以一种符合我们早期价值观的方式翻身的。那些价值观包括产品设计如何达到卓越,卓越到人们都对这个产品垂涎三尺。这种价值观也是关于情感的,一种愉快的情感。
如果你像我这么幸运,你将生活在这样一个时代:一次革新即将开始,而你正当年少。如同亨利·福特与汽车产业,我与第一台个人电脑。
我希望你也像我一样幸运。这个世界需要发明者——好的发明者。你可以成为这样的人。如果你热爱你做的事,愿意付出相应的劳动,你将终有所得。你在夜里独自工作,反复思考你想设计与制造的东西,为之花费的每一分钟都是值得的。
我敢肯定的告诉你,你的付出是值得的。